Littlewood's rule
The earliest Revenue Management model is known as Littlewood’s rule.
The two class model
Littlewood proposed the first static single resource quantity based RM model [1]. It was a solution method for the seat inventory problem for a single leg flight with two fare classes. Those two fare classes have a fare of  1 and
1 and  2, whereby
2, whereby  1 >
1 >  2. The total capacity is
2. The total capacity is  and demand for class
and demand for class  is indicated with
is indicated with  j. The demand is distributed via a distribution that is indicated with
j. The demand is distributed via a distribution that is indicated with  j
j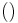 . The demand for class 2 comes before demand for class 1. The question now is how much demand for class 2 should be accepted so that the optimal mix of passengers is achieved and the highest revenue is obtained. Littlewood suggests closing down class 2 when the certain revenue from selling another low fare seat is exceeded by the expected revenue of selling the same seat at the higher fare [2]. In formula form this means: accept demand for class 2 as long as:
. The demand for class 2 comes before demand for class 1. The question now is how much demand for class 2 should be accepted so that the optimal mix of passengers is achieved and the highest revenue is obtained. Littlewood suggests closing down class 2 when the certain revenue from selling another low fare seat is exceeded by the expected revenue of selling the same seat at the higher fare [2]. In formula form this means: accept demand for class 2 as long as:
 2
2 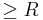 1
1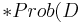 1
1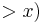
where
 2 is the value of the lower valued segment
2 is the value of the lower valued segment 1 is the value of the higher valued segment
1 is the value of the higher valued segment 1 is the demand for the higher valued segment and
1 is the demand for the higher valued segment and is the capacity left
is the capacity left
This suggests that there is an optimal protection limit  1*. If the capacity left is less than this limit demand for class 2 is rejected. If a continuous distribution
1*. If the capacity left is less than this limit demand for class 2 is rejected. If a continuous distribution  j
j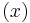 is used to model the demand, then
is used to model the demand, then  1* can be calculated using what is called Littlewood’s rule:
1* can be calculated using what is called Littlewood’s rule:
 1*
1*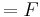 1-1
1-1 2
2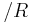 1
1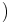
This gives the optimal protection limit, in terms of the division of the marginal revenue of both classes.
Alternatively bid prices can be calculated via
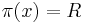 1
1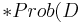 1
1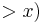
Littlewood's model is limited to two classes. P. Belobaba developed a model based on this rule called Expected marginal seat revenue, abbreviated as EMSR, which is an  -class model [3]
-class model [3]
References
- ^ Pak, K. and N. Piersma (2002). Airline Revenue Management: An overview of OR Techniques 1982-2001. Rotterdam, Erasmus university
- ^ Littlewood, K. (1972). "Forecasting and Control of Passenger Bookins." AGIFORS Symposium Proc. 12
- ^ Belobaba, P. P. (1987). Air Travel Demand and Airline Seat Inventory Management. Flight Transportation Laboratory. Cambridge, MIT. PhD